まず、球の表面を縦に均等に割ってみることにした。
つまり、地球でいうと北極から南極にかけて線を引いて分けるということだ。(同じ経度で線を引く)
このとき、一つの切り口(切れ長の目のような形になる)を菱形と見なして計算してみた。
菱形の縦の長さは、円周の半分なのでπr。
菱形の横の長さは、円周のn等分した長さなので、2πr/n。
よって菱形一つの面積は、2(π^2)(r^2)/n。
これがn個あるわけなので、表面積は2(π^2)(r^2)となる。
…これは違う。菱形に近似したのがいけなかったのか。
別の方法を考えた。
今度は、リンゴの皮むきのように横に切ってみることにした。
地球で言うと、同じ緯度で線を引いて分ける。
北半球だけで考える。北半球をn等分する。
下から(赤道から)t番目(0<=t
これは上下の長さの違う円筒の形だが、結局長方形と見なせる。
上辺と下辺の長さは違うが、どうせあとでnを無限に大きくするので、長さは同じとみなしちゃって大丈夫。
とりあえず下辺の長さを使う。下図で青い三角形の三平方の定理を使う。
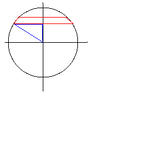
青三角形の縦の長さは、r(t/n)。
ナナメの長さはr。
よって、横の長さはr(n^2 - t^2)/n。
下辺の周の長さは、2π × r(n^2 - t^2)/n。
だから、赤いところの面積は、 2π × r(n^2 - t^2)/n × r/n。
これを全部足すと、2π × Σ(r(n^2 - t^2)/n × r/n)となる。(t=0->n-1)
計算すると、
n-1 r (n^2 - t^2) × r
2π × Σ ( ------------------------)
t=0 n × n
n-1 (n+t)(n-t)
= 2π r^2 × Σ ( ------------- )
t=0 n × n
n-1 t t
= 2π r^2 × Σ ( 1 + - ) (1 - - )
t=0 n n
ここで、nを無限に大きくすると、Σの中身は1になる。
だから、2π r^2となる。
これは北半球だけの面積なので、南半球も含めると、4π r^2となる。
合ってるかな?
最後のところとか大丈夫だろうか。
答えを知ってるから繋げられたところもあるけど。
PR

